1. Прокляття розмірності
Людина еволюціонувала в 3 просторових вимірах, і в них ми себе чудово почуваємо. У них ми живемо, радіємо, сумуємо, та й усі драми життя відбуваються в цих вимірах. Щоправда, в першій половині 20 століття Теодор Калуза і Оскар Клейн знайшли ще один вимір, але він маленький і людям його не видно. Після струнні теоретики, такі як Леонард Сасскінд, Герард т'Хофт, Яу Шінтун, Олександр Віленкін та інші, знову сильно ускладнили картину світу, і до 4 просторових вимірів додали ще 6 (це мінімум), але вони всі десь невідомо де, і впливають на життя тільки фізиків-теоретиків, а решті n-мільярдів людей на Землі немає ніякої справи до цих вимірів, їм і в 3 добре живеться.

Інша справа математика і наука про дані, тут вимірів може бути скільки завгодно, наприклад ось:
df = pd.DataFrame({
"age": np.random.randint(18, 60, n_samples), # вік
"height": np.random.randint(150, 200, n_samples), # зріст
"weight": np.random.randint(50, 100, n_samples), # вага
"gender": np.random.choice(["male", "female"], n_samples), # категорійний
"city": np.random.choice(["Berlin", "Paris", "London", "Rome"], n_samples), # категорійний
"education": np.random.choice(["highschool", "bachelor", "master", "phd"], n_samples),
"occupation": np.random.choice(["engineer", "teacher", "doctor", "artist"], n_samples),
"hobby": np.random.choice(["sports", "music", "gaming", "reading"], n_samples),
"married": np.random.choice(["yes", "no"], n_samples),
"children": np.random.randint(0, 4, n_samples) # числовий
})
DataFrame згенеровано ChatGPT
Це синтетичний датафрейм, і в ньому 10 вимірів: кожна ознака — така як age, height і т. д. — представляє собою окремий вимір. Але тут і починаються проблеми. У реальних проєктах число вимірів може досягати сотень або навіть тисяч, і людині в силу природи важко осмислити і впорядкувати таку інформацію. Крім того, виникає серйозна проблема з візуалізацією: на звичному двовимірному графіку дані виявляються «розмазаними» і не дають розуміння, які класи близькі один до одного.
Перш ніж продовжити, нам треба розібрати одну важливу частину — евклідова відстань, тобто найкоротший шлях по прямій між двома точками. Чому це важливо? У звичній декартовій системі координат (графік з осями X і Y) саме ця метрика дає природне уявлення про те, які об'єкти ближчі один до одного. Інші відстані, такі як манхеттенська або Чебишева, застосовні в інших задачах, але для візуалізації вони мало допомагають.
Формально евклідова відстань обчислюється як корінь із суми квадратів різниць за кожним виміром. Але в високих розмірностях навіть невеликі відмінності за багатьма координатами накопичуються, і всі відстані починають вирівнюватися. У результаті найближчий сусід виявляється майже так само далеким, як і найвіддаленіший об'єкт. Дані «розповзаються» по кутах багатовимірного простору, і на візуалізації ми бачимо лише рівномірну хмару точок без структури.
Давайте запишемо формулу евклідової відстані, щоб краще зрозуміти її. Ось у нас є таблиця
age | height | weight |
25 | 180 | 75 |
30 | 175 | 70 |
Тоді:


Як видно, обчислення нескладне, особливо якщо у нас всього дві рядки даних. Але вже при десятках ознак і тисячах об'єктів краще використовувати готові бібліотеки, щоб уникнути помилок і заощадити час.
Повертаємося до візуалізації. Якщо спробувати побудувати scatter-графік для датафрейму з початку статті, то вийде наступне:
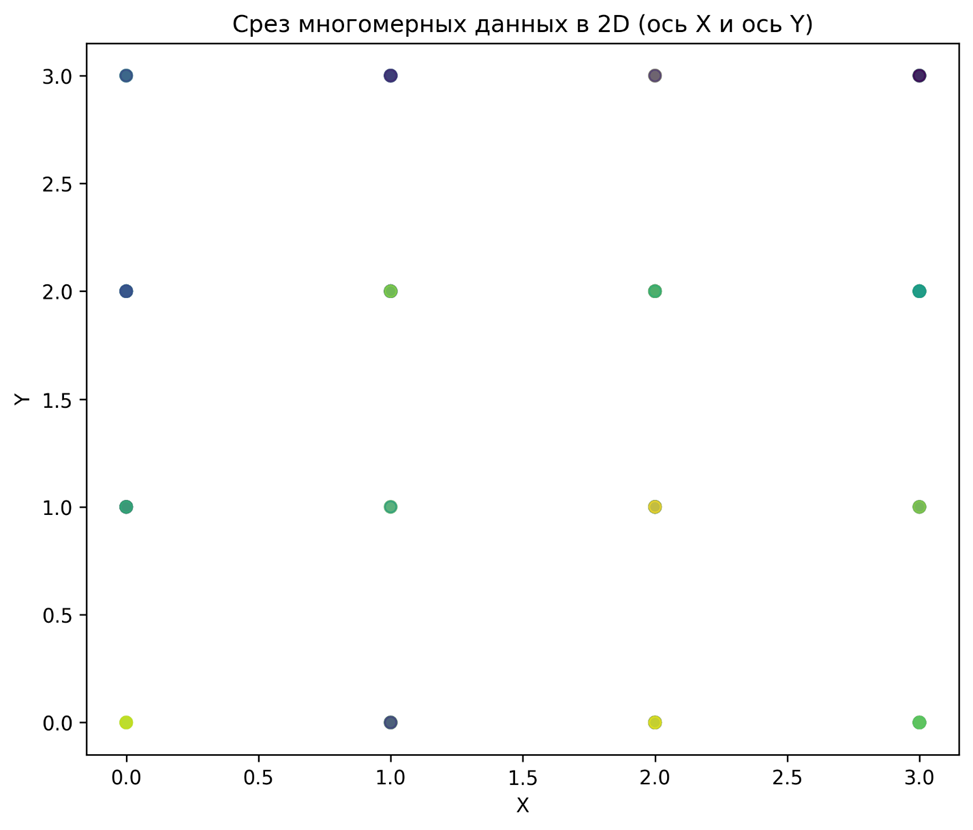
Дивлячись на графік, ми не можемо зрозуміти, які класи дійсно сусідують, а які розділені.
2. Як позбутися прокляття
Велика розмірність даних — це не вирок. Так, існують класичні методи зниження розмірності, такі як PCA і LDA. Про них написано безліч книг і статей, тому я не буду повторюватися. Тут я хочу розповісти про інший підхід — метод, який не зводить дані до лінійних комбінацій ознак, а допомагає побачити їхню структуру в звичних двох або трьох вимірах. Цей метод називається t-SNE, і про нього, принаймні мені, зустрічалося набагато менше матеріалів.
t-SNE відмінно працює зі складними наборами даних. Він дозволяє візуалізувати їх у 2D або 3D так, щоб зберегти локальну структуру. Інтуїтивно принцип роботи такий: алгоритм оцінює відстані між точками в початковому багатовимірному просторі і на їхній основі обчислює ймовірність того, що об'єкти є сусідами. Потім він підбирає таке розташування точок у 2D/3D, щоб ці ймовірності якнайточніше зберігалися.
Спрощено процес можна описати так:
1. Обчислюємо ймовірність того, що в початковому просторі точки є сусідами.
2. Стискаємо простір у 2D або 3D. У новому просторі близькість точок моделюється через t-розподіл Стьюдента з одним ступенем свободи.
3. Мінімізуємо розбіжність: прагнемо, щоб сусіди в початковому просторі залишалися сусідами і в новому. Для цього використовується дивергенція Кульбака–Лейблера.
4. Оптимізуємо: застосовуємо стохастичний градієнтний спуск, щоб знайти таке розташування точок, при якому функція помилки мінімальна.
У цьому поясненні я свідомо не використав формули, бо мета статті — не математичний розбір t-SNE, а знайомство з зручним способом візуалізації даних. У реальному житті навряд чи комусь доведеться писати цей алгоритм з нуля, зате з бібліотекою scikit-learn працювати з ним не робота, а суцільне задоволення. Нижче я покажу приклад з її допомогою, використовуючи вбудований датасет load_digits, який застосовується для задач класифікації рукописних цифр.
import matplotlib.pyplot as plt
from sklearn.datasets import load_digits
from sklearn.preprocessing import StandardScaler
from sklearn.manifold import TSNE
# 2. Завантаження набору даних (цифри 0–9, 64 ознаки — зображення 8x8)
data = load_digits()
X = data.data # ознаки
y = data.target # мітки класів
# 3. (Рекомендовано) Стандартизація ознак
scaler = StandardScaler()
X_std = scaler.fit_transform(X)
# 4. Застосування t-SNE
tsne = TSNE(n_components=2, perplexity=30, max_iter=500, random_state=42)
X_tsne = tsne.fit_transform(X_std)
# 5. Візуалізація
plt.figure(figsize=(10, 6))
scatter = plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y, cmap='tab10', s=20, alpha=0.8)
plt.colorbar(scatter, label="Клас (цифра)")
plt.title('t-SNE проекція даних (Digits Dataset)')
plt.xlabel('t-SNE 1')
plt.ylabel('t-SNE 2')
plt.grid(True)
plt.tight_layout()
plt.show()
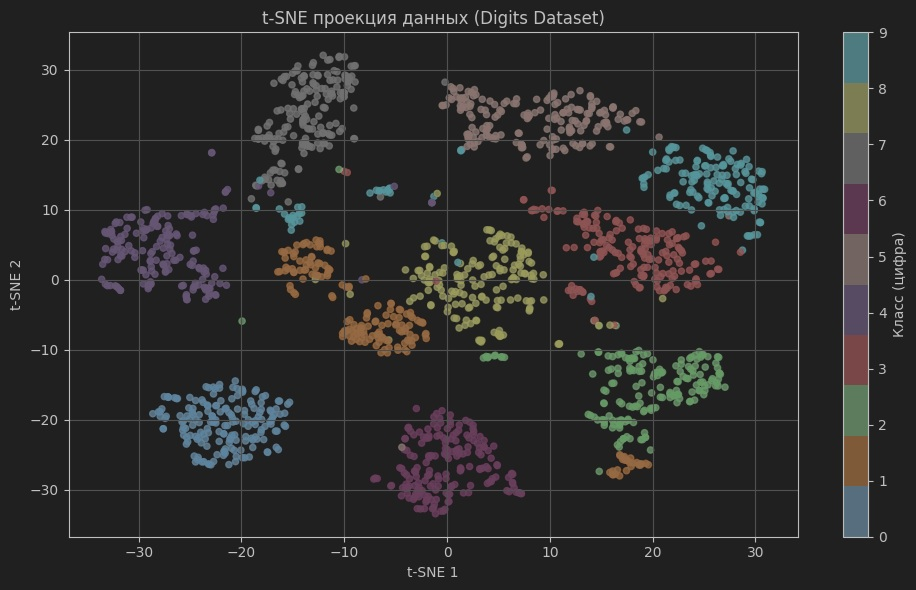
t-SNE проекція даних: алгоритм звів 64 ознаки зображень цифр у двовимірний простір. Видно 10 чітких кластерів, що відповідають цифрам 0–9.
Тепер давайте поговоримо про гіперпараметри t-SNE:
1. n_components – розмірність нового простору. Зазвичай використовують 2 (для плоскої картинки) або 3 (для тривимірної візуалізації). Більше майже ніколи не має сенсу.
2. perplexity – число «ефективних сусідів». Мале значення (5–10) акцентує локальні зв'язки, в результаті виходить багато дрібних кластерів. Велике значення (40–50) дає більш глобальну картину, кластери можуть зливатися. Зазвичай використовують діапазон 5–50.
3. max_iter(n_iter – залежить від версії бібліотеки) – кількість ітерацій градієнтного спуску. Мале значення - результат сирий і нестійкий. Велике - якісніше, але повільніше. Зазвичай 500–1000 достатньо.
4. random_state – Стандартний гіперпараметр scikit-learn, використовується для того, щоб результат був однаковим при кількох запусках коду .
5. learning_rate – швидкість навчання. Якщо занадто мала, алгоритм сходиться повільно і може «злипнути» точки. Якщо занадто велика, точки «розлітаються хаотично». Зазвичай вибирають у діапазоні 10–1000, за замовчуванням auto.
6. metric – метрика відстані в початковому просторі. За замовчуванням використовується евклідова, але можна пробувати й інші (косинусна, манхеттенська і т. д.).
7. early_exaggeration – параметр, який штучно збільшує відмінності між точками на перших ітераціях, допомагаючи кластерам розійтися. Зазвичай за замовчуванням 12.0.
3. Це ж навчання без учителя!?
І так, і ні. Формально t-SNE відноситься до методів навчання без учителя, бо він працює без заздалегідь заданих міток класів. Алгоритм дійсно «нічого не знає» про зміст даних: йому байдуже, цифри це, молекули чи тексти. Він бачить тільки відстані між точками і намагається зберегти їхнє відносне положення. Простіше кажучи, t-SNE будує топологічну карту даних — показує форму рельєфу: де «височини» (щільні кластери), а де «долини» (рідкісні області).
Але важливо розуміти відмінність від алгоритмів кластеризації, таких як k-means або DBSCAN.
t-SNE лише показує геометрію — хто з ким поруч, але не каже: «це кластер номер 1, це кластер номер 2». Кластеризація йде далі: вона намагається розділити простір і присвоїти кожній точці ярлик (хай і умовний).
Таким чином, t-SNE — це інструмент для візуального аналізу, свого роду карта рельєфу багатовимірного простору. Він не вирішує задачу класифікації, але допомагає людині «побачити» структуру даних. А вже поверх цієї карти можна застосовувати алгоритми кластеризації або навчання з учителем, якщо потрібно формальне розділення.
4. Майбутнє візуалізації даних
Нещодавно я задумався про те, що геометрія і, в більшій мірі, топологія як раз і займаються тим, що знайомлять людину з тим, як виглядає простір. Наприклад, потоки Річчі — це спосіб еволюції метрики, який дозволяє «розгладити» поверхню і зрозуміти її структуру. У XX столітті цей підхід застосували Калабі і Яу, щоб описати особливі багатовимірні об'єкти, відомі як, власне, простори Калабі–Яу.
Цікаво, що сьогодні потоки Річчі вже почали застосовувати в експериментах у Data Science. І це наводить на думку: багато методів з теоретичних областей математики, таких як геометрія і топологія, цілком можуть знайти своє місце в машинному навчанні. Ми поки використовуємо тільки частину можливих інструментів, але горизонти тут величезні.
Коментарі