Це літо порадувало нас проривом в обробці зображень за допомогою нейромереж. Одна за іншою виходять такі моделі, як Flux.1 Kontext, Qwen-Image-Edit, Gemini 2.4 Flash Image Preview (Nano Banana), демонструючи недосяжний досі рівень маніпуляції цифровим контентом. Це не заміна Photoshop, а технологія, що відкриває ворота в нескінченні візуальні світи, і все завдяки потужності Diffusion Transformer (DiT) архітектури. Вражений, я вирішив ближче познайомитися з дифузійними трансформерами — власноруч навчити свою власну DiT-модель. Про це й буде ця стаття.
Але почати варто з малого.
Базова модель
Як взагалі працюють ці дифузійні моделі? Є нейромережа, яка приймає на вхід зашумлене зображення, а на виході видає шум (noise). І виникає питання, навіщо нам цей шум? А потім, маючи шумне зображення і передбачений шум, ми можемо відняти передбачений шум від зображення і отримати зображення з меншою кількістю шуму. Я щойно сказав «з меншою кількістю шуму», але насправді це не так. Насправді все складніше.
Невеликий відступ. Для створення моделі я буду використовувати бібліотеку PyTorch. Усі терміни, такі як тензор (tensor), батч (batch), вимір (dimension), шейп (shape), звідти. Очікую від читачів хоча б поверхневого розуміння.
А що моделюємо?
Ви не задумувалися, що взагалі моделюють дифузійні моделі? А моделюють вони трансформацію нормального розподілу в цільовий розподіл. Виникає логічне питання: що ще за «цільовий розподіл»? Найлегше це проілюструвати на прикладі двох вимірів. Ось кілька семплів (точок на координатній площині) з нормального розподілу. Відтепер і далі, коли я пишу «семпл», то маю на увазі двовимірний тензор, який можна представити як точку на координатній площині:
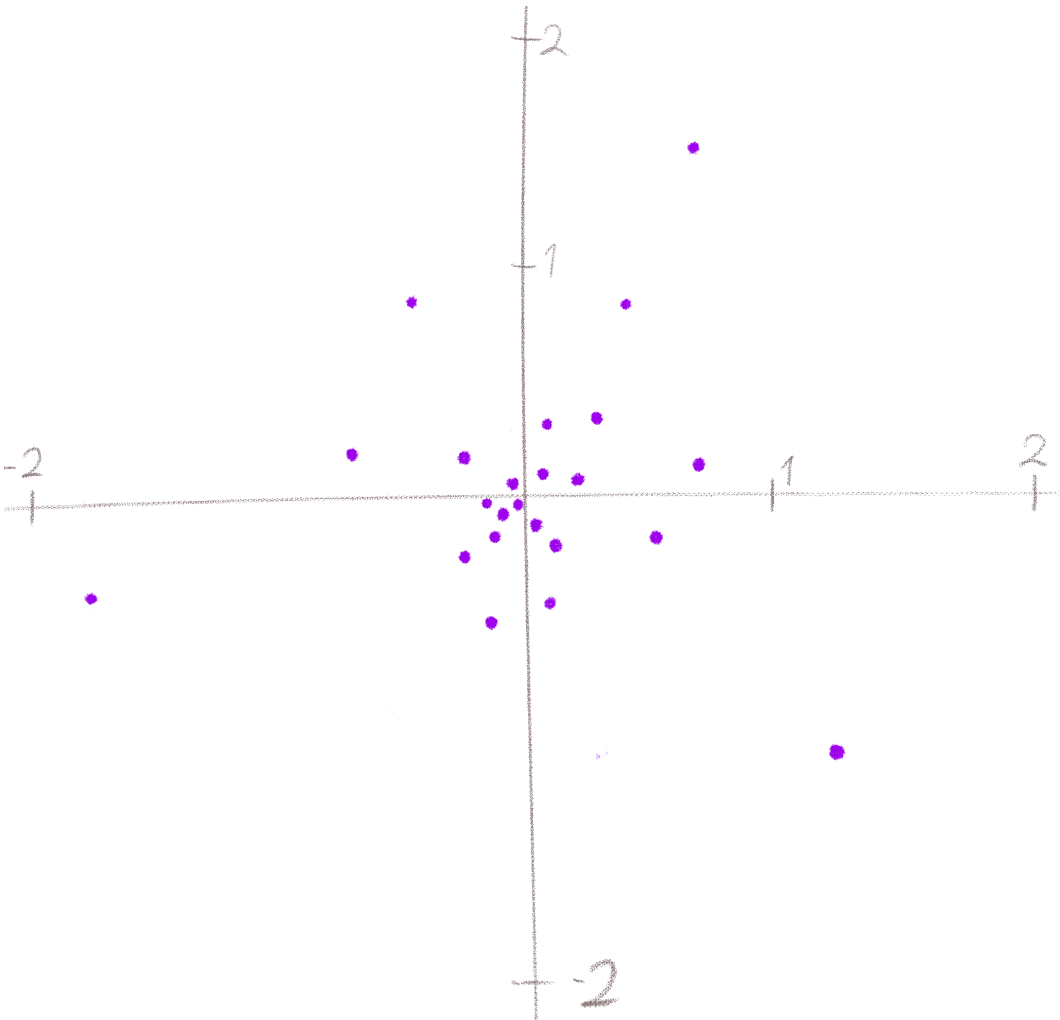
Семпли з нормального розподілу отримати дуже просто — викликаємо torch.randn(2) скільки треба разів і все.
А ось так на координатній площині могли б виглядати семпли з цільового розподілу:
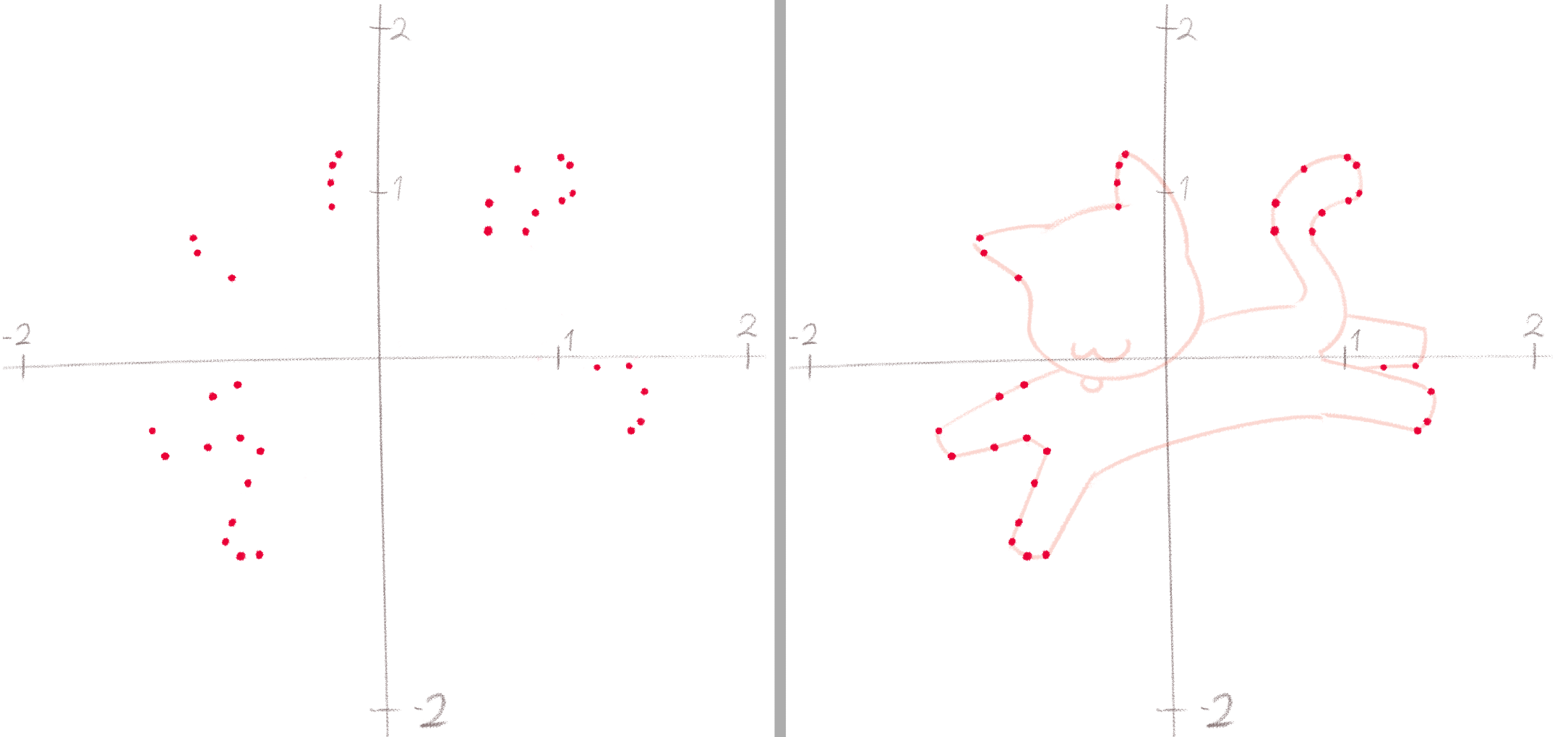
Цей розподіл можна визначити як «всі точки, що лежать на кривих, які утворюють малюнок кошеняти». На відміну від нормального розподілу у нас немає готової формули, яка б могла витягувати точки (семпли) саме з цього розподілу.
І тут усім любителям котів на допомогу приходять нейромережі. Лише треба навчити функцію (модель), яка приймає на вхід семпл з нормального розподілу, а повертає семпл вже з цільового розподілу. Ось тільки така постановка завдання — повертати семпли цільового розподілу — занадто складна. Тому трохи перефразуємо:
Приймаючи на вхід семпл з нормального розподілу, повертати вектор напрямку, рухаючись по якому ми досягнемо цільового розподілу.
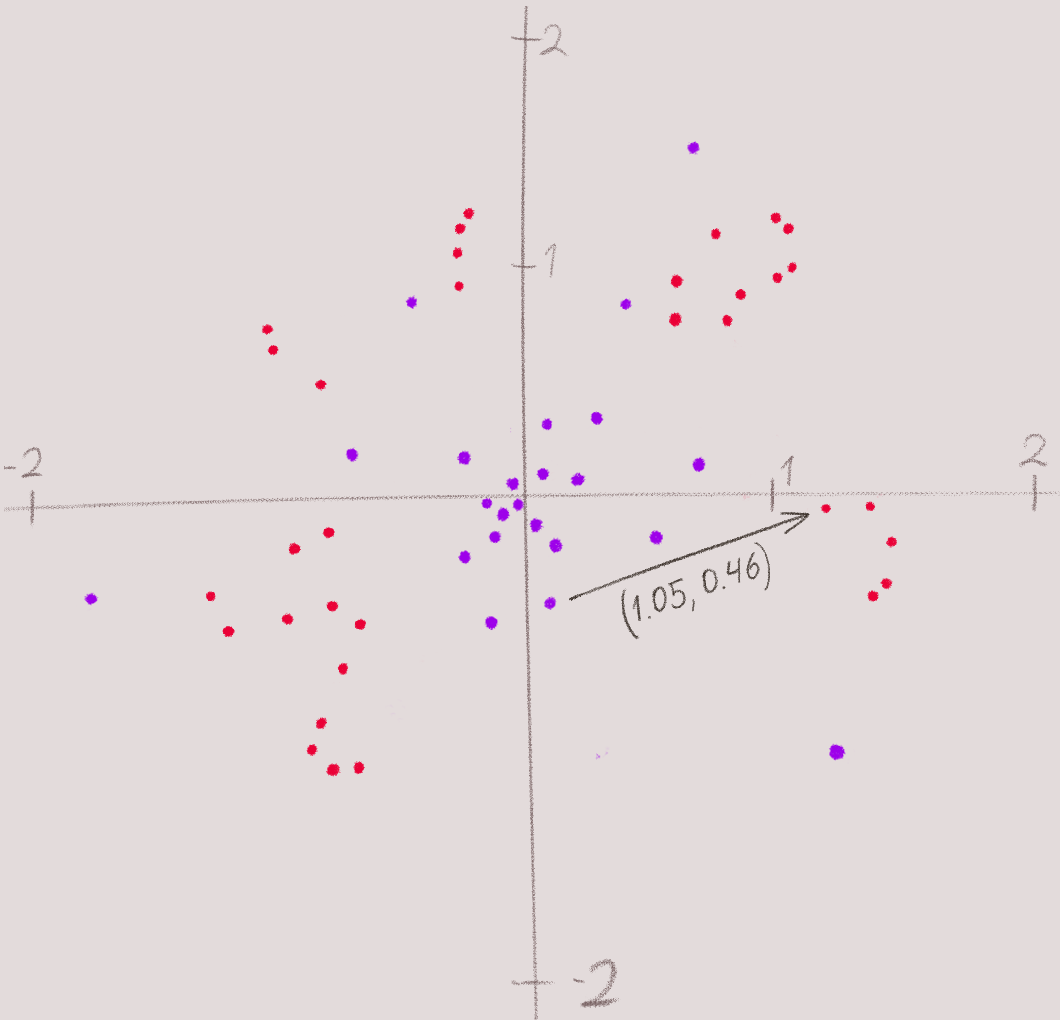
Виходить, що, наприклад, для семпла (0.1, -0.5) наша модель передбачить вектор (1.05, 0.46). Тепер складемо цей вектор з вихідним семплом. Отримуємо точку на цільовому розподілі. І так буде працювати для кожного семпла з нормального розподілу.
Те, що я щойно описав (передбачення вектора) — це варіант дифузії, що називається Rectified Flow. Він відрізняється від відомого всім DDPM і відрізняється в кращу сторону. Але я про це рано заговорив, продовжуємо.
Отже, можна сказати, що наша модель буде моделювати трансформацію простого розподілу (нормальний, він же гауссів) в складний цільовий розподіл.
Звучить добре, та ось тільки моделювати трансформацію в один крок — це важкувата задача виходить. Он GAN-моделі з таким підходом далеко не просунулися. Гаразд, з GAN-моделями я трохи перебільшую, але набагато практичніше спиратися саме на траєкторію — як крок за кроком просте розподіл трансформується в складне.
Що я маю на увазі, коли кажу, що можна спиратися на траєкторію? Дивіться, спочатку дані для тренування нашої нейромережі складалися тільки з семплів цільового розподілу (точки, що лежать на графіку кота), а також такої ж кількості семплів з нормального розподілу (шуму коротше). Але раз ми здогадалися моделювати трансформацію розподілу «по кроках», то ми можемо збагатити наш датасет усіма проміжними станами, тобто цільовими семплами, які зашумлені на 10%, 20%, 76% або взагалі на будь-який відсоток. Іншими словами, точками, які знаходяться десь на півдорозі між нормальним розподілом і цільовим.
Давайте ще раз подивимося, як підхід «вивчити траєкторію за раз» і «вивчити траєкторію по кроках» змінює нашу модель.
У першому випадку наша модель функціонує ось так:vector_to_target = model.predict(normal_noise_sample) — на вхід тільки семпл з нормального розподілу.
А в разі траєкторії по кроках модель буде працювати так:vector_to_target = model.predict(point_between_noise_and_target_distribution, time)
Тут time — це частка шляху, який точка пройшла від шуму до цільового розподілу. Відсоток зашумленості, іншими словами. Важливо розуміти: по суті, задача трансформації розподілу розбивається на дрібні підзадачі: «навчися передбачати шлях до цільового розподілу при 10% шуму», «навчися передбачати шлях до цільового розподілу при 15% шуму» і т.д. Такий підхід дозволяє набагато краще змоделювати трансформацію розподілів, що підвищує точність «передбачення».
За рахунок чого збільшується точність? А за рахунок того, що тепер маючи модель з додатковою умовою time ми можемо витягувати семпли з цільового розподілу не з єдиної спроби, а роблячи скільки завгодно «уточнень» траєкторії. Легше зрозуміти, якщо поглянути на код інференсу:
noise = sample_noise() # семпл з нормального розподілу
steps = 200 # розіб'ємо траєкторію на 200 маленьких кроків
for step in range(steps):
time = step / steps # змінюватиметься в інтервалі [0, 1)
# незалежно від time цей вектор завжди однієї довжини
# в ідеалі взагалі завжди один і той самий
predicted_vector = model.predict(noise, time)
scaled_vector = predicted_vector * (1 / steps) # одна 200-та шляху
noise = noise + scaled_vector # Наш початковий шум на 0.5% наблизився
# до цільового розподілу
# Після завершення циклу наш noise — це вже семпл з цільового розподілу
Пам'ятайте, що в нашому прикладі всі семпли це двовимірні вектори (x, y) — точки на площині. Користуючись термінологією PyTorch — тензори з шейпом (2). А так-то модель можна створювати для тензорів будь-якої форми.
Досить теорії
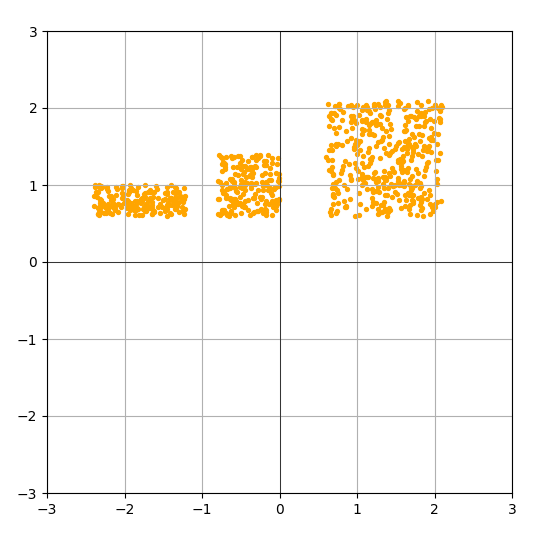
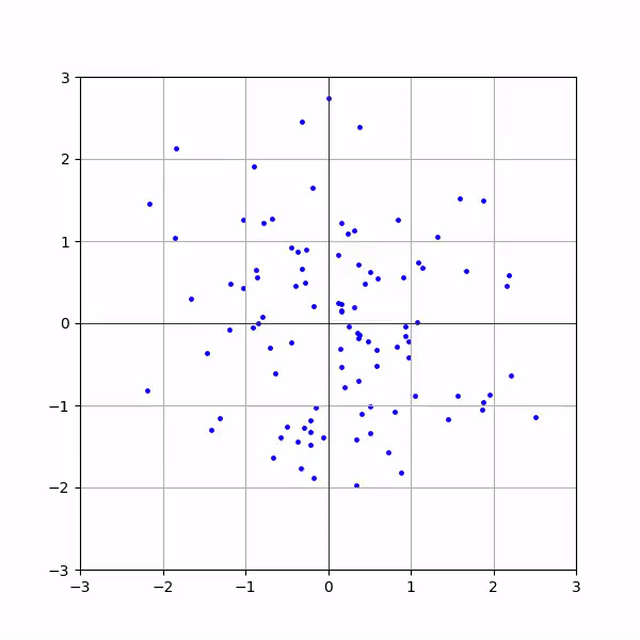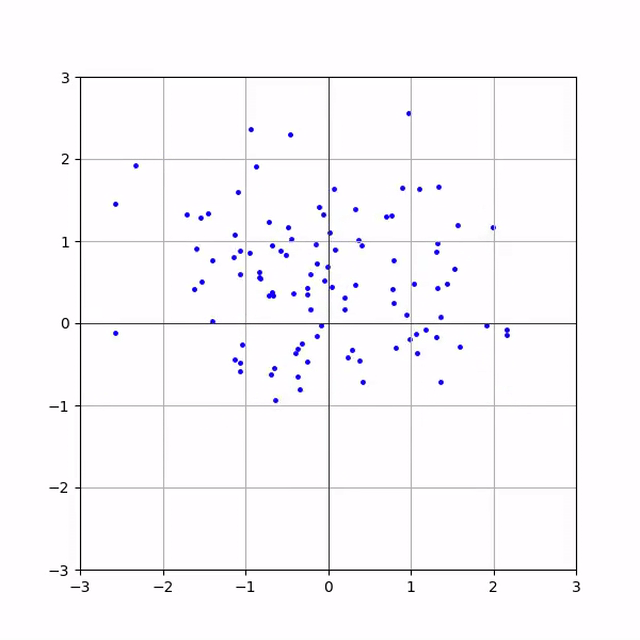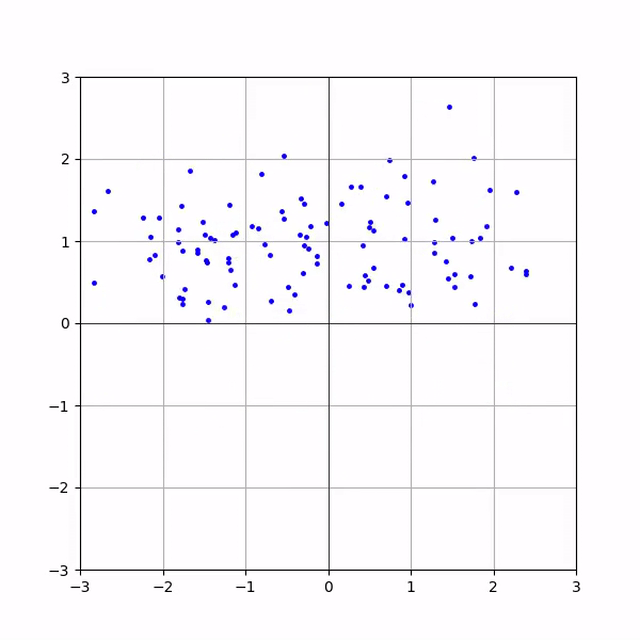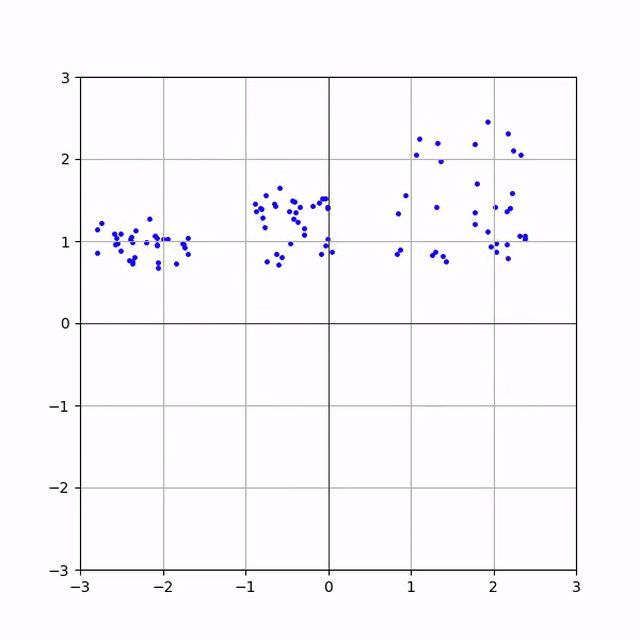
Для демонстрації нам знадобиться датасет. Усі елементи з нього будуть вважатися семплами з цільового розподілу. Наприклад ось такого:
def make_simple_dataset(amount):
cluster_1 = torch.rand((amount // 2), 2) * 1.5 + 0.6
cluster_2 = torch.rand((amount // 4), 2) * 0.8 + torch.tensor([-.8, .6])
cluster_3 = torch.rand((amount // 4), 2) * torch.tensor([1.2, 0.4]) + torch.tensor([-2.4, 0.6])
return torch.cat([cluster_1, cluster_2, cluster_3], dim=0)
На координатній площині 800 семплів цього розподілу будуть виглядати ось так:
Тепер пора братися за PyTorch модель.
Буде ця модель складатися з трьох частин:
- Енкодер, який проєктує вхідний вектор з двох вимірів у внутрішній вектор з більшої кількості вимірів (16). Навіщо нам більша кількість вимірів? Щоб моделі було де «розвернутися».
- Основна модель, що складається з кількох MLP-блоків. Буде безпосередньо займатися денойзингом вхідних «шумних» семплів. MLP — це multilayer perceptron, та сама «класична» нейронна мережа.
- Декодер, який перетворює 16-розмірний вектор назад у дві координати.
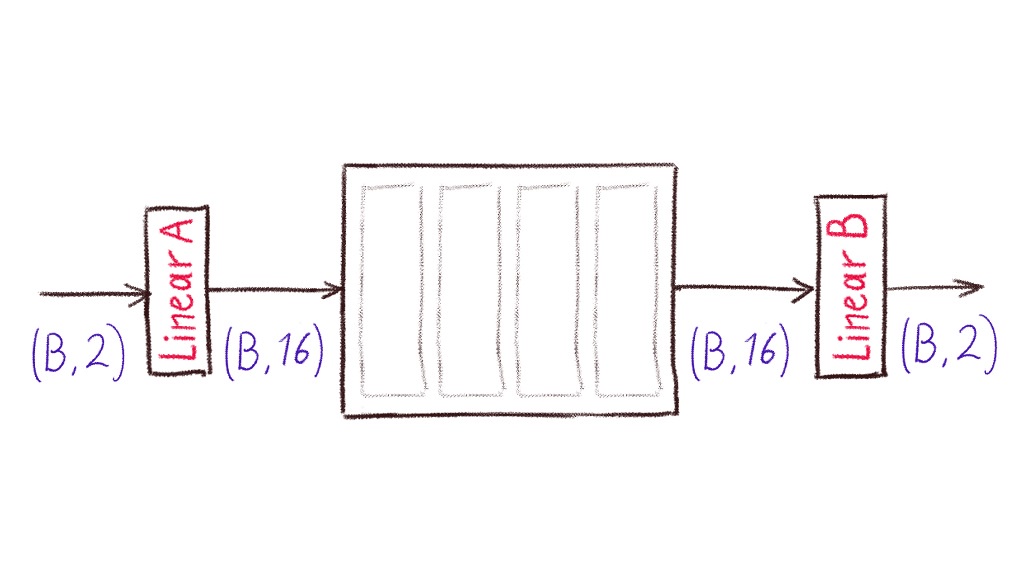
Ось так виглядає спрощена схема. Linear A — це енкодер. Складається з одного єдиного шару nn.Linear (тут і далі всі типи з PyTorch). По суті просто матриця, для трансформації 2-розмірного тензора в 16-розмірний. Прямокутник посередині — це сам денойзер, що складається з кількох послідовних блоків/рівнів. Кілька невеликих нейромереж, вибудуваних в ряд, коротше. Linear B — це декодер. Знову ж, матриця для трансформації 16-розмірного тензора назад у 2 координати на площині. На схемі разом 2 і 16 написано (B, 2) і (B, 16), тому що модель приймає на вхід семпли не по одному, а відразу групою (батчем). B — це розмір батча (кількість елементів).
Давайте відразу розберемо, як влаштовані внутрішні блоки. Заодно згадаємо, як зробити в PyTorch Multilayered perceptron.
Отже, як написати ось таку нейромережу (модель)?
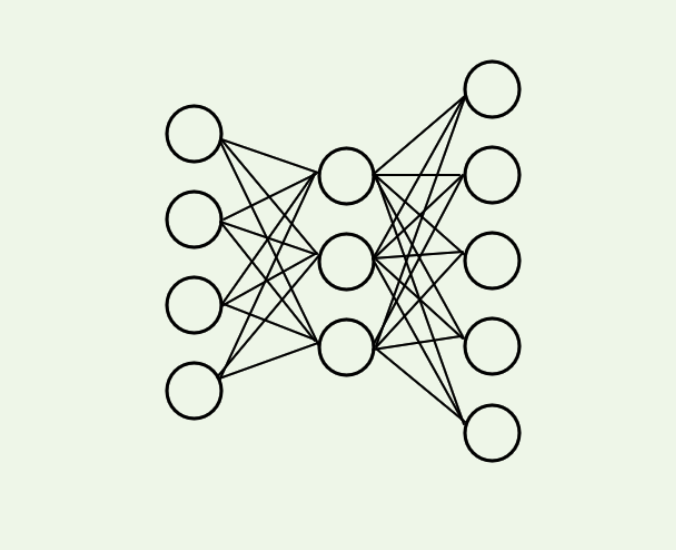
На PyTorch простіше простого:
model = nn.Sequential(
nn.Linear(4, 3), # повнозв'язний шар
nn.SiLU(), # функція активації
nn.Linear(3, 5), # повнозв'язний шар
)
Давайте тільки загорнемо це в окремий клас:
class MyBlock(nn.Module):
def __init__(self):
super().__init__()
self.mlp = nn.Sequential(
nn.Linear(4, 3),
nn.SiLU(),
nn.Linear(3, 5),
)
def forward(x): # ця функція пропускає вхідні дані крізь нашу модель
return self.mlp(x)
nn.Module — це корисний клас, який полегшує подальшу роботу з моделлю.
Думаю, код буде гнучкішим, якщо винести скалярні константи в конструктор:
class MyBlock(nn.Module):
def __init__(self, hidden_dim, mlp_ratio):
super().__init__()
self.mlp = nn.Sequential(
nn.Linear(hidden_dim, hidden_dim * mlp_ratio),
nn.SiLU(),
nn.Linear(hidden_dim * mlp_ratio, hidden_dim),
)
def forward(x):
return self.mlp(x)
Тепер «ширину» і розмірність вхідного вектора для цієї нейромережі можна вказувати при створенні.
Повний код
import torch.nn as nn
class DenoiserBlock(nn.Module):
def __init__(self, hidden_dim, mlp_ratio):
super().__init__()
self.ln = nn.LayerNorm(hidden_dim)
self.mlp = nn.Sequential(
nn.Linear(hidden_dim, hidden_dim * mlp_ratio),
nn.SiLU(),
nn.Linear(hidden_dim * mlp_ratio, hidden_dim),
)
def forward(self, x):
z = self.ln(x) # спочатку проганяємо вхідний тензор крізь нормалізацію
return self.mlp(z) # а потім крізь MLP
В результаті вийшла модель внутрішнього блоку, з яких буде складатися наша основна модель-денойзер. Так, а звідки взявся nn.LayerNorm? Зараз вдаватися в подробиці не буду, просто скажу, що nn.LayerNorm дозволяє утримувати значення тензорів (точок) десь в межах [-2, 2].
Ось для прикладу дані до і після нормалізації
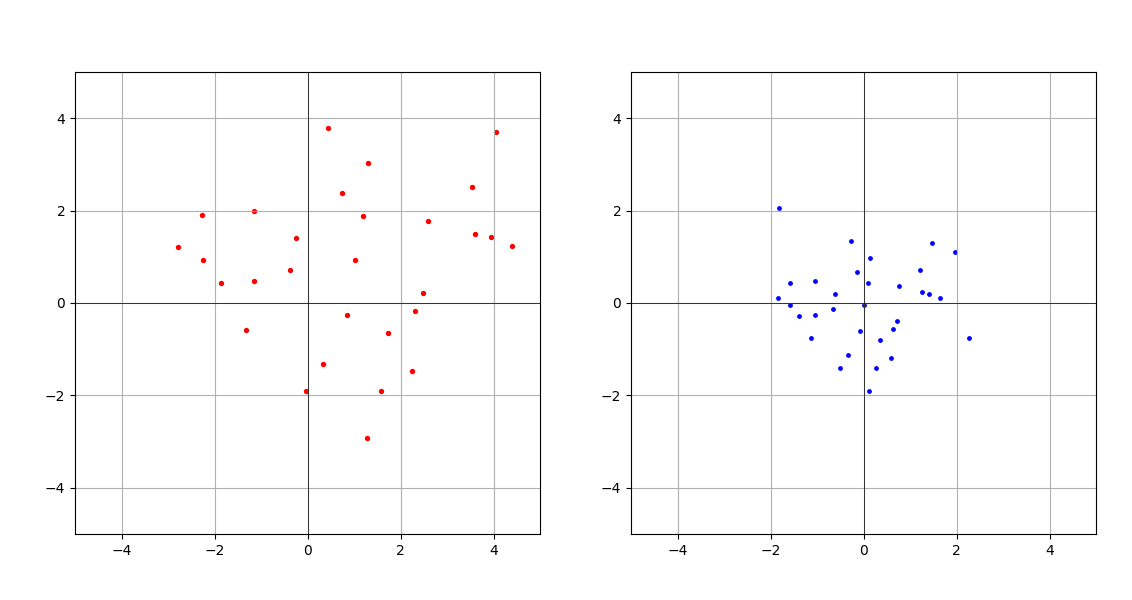
Іншими словами, нормалізувати — це значить перетворити дані так, щоб середня була 0, а стандартне відхилення 1. Звичайна формула зі статистики. Таким чином nn.LayerNorm полегшує тренування моделі і має ще одну корисну властивість, про яку я, можливо, розповім пізніше.
До речі, питання до зали: тензор якої форми зможе приймати на вхід ось ця конкретна модель:
model = DenoiserBlock(25, 3)
Відповідь: будь-який тензор, у якого останній вимір дорівнює 25. Наприклад (25), (72, 25), (1, 25), (8, 3, 25, 25), і т.п.
Гаразд, з єдиним блоком розібралися, переходимо до основної моделі.
class Denoiser(nn.Module):
def __init__(self, hidden_dims):
super().__init__()
self.input_encoder = nn.Linear(2, hidden_dims)
self.blocks = []
self.output_decoder = nn.Linear(hidden_dims, 2)
Як і на схемі вище, шар для перетворення вхідного 2-розмірного тензора в 16-розмірний, шар для перетворення внутрішнього 16-розмірного тензора назад у 2-розмірний. Давайте ще раз нагадаю, що тут 2-розмірний тензор це тензор з шейпом (розміром) (B, 2), а 16-розмірний з шейпом (B, 16). Тут B — це розмір батча (групи). Скільки семплів (точок) ми обробляємо за раз, іншими словами. Якщо, наприклад, вхідний тензор буде розміром (64, 2), то пройшовши через input_encoder він перетвориться в тензор (64, 16).
Додаємо внутрішні блоки:
class Denoiser(nn.Module):
def __init__(self, hidden_dims, num_blocks):
super().__init__()
self.input_encoder = nn.Linear(2, hidden_dims)
block_list = [DenoiserBlock(hidden_dims, 4) for _ in range(num_blocks)]
self.blocks = nn.ModuleList(block_list)
self.output_decoder = nn.Linear(hidden_dims, 2)
Навіщо обгортати в nn.ModuleList? Все для того, щоб параметри всіх внутрішніх моделей в списку були доступні зовнішній моделі. Іншими словами, щоб Denoiser зі списком DenoiserBlock всередині управлявся як єдина модель.
Залишилося тільки дописати метод forward
def forward(self, x):
hidden = self.input_encoder(x) # (B, 2) -> (B, 16)
for block in self.blocks:
hidden = block(hidden) # вихід одного блоку передається на вхід другому
return self.output_decoder(hidden) # (B, 16) -> (B, 2)
А код-то неправильний! Блоки всередині денойзера повинні бути з'єднані не послідовно, а через skip-connection. Не забувайте, що кінцева мета — це модель-трансформер, а у трансформерів шари (блоки) з'єднані через skip-connection, тому переробляємо те, як з'єднані блоки і перетворюємо Denoiser в залишкову мережу:
def forward(self, x):
hidden = self.input_encoder(x) # (B, 2) -> (B, 16)
for block in self.blocks:
# Вихід кожного блоку додається до початкового представлення і передається далі
hidden = hidden + block(hidden) #
return self.output_decoder(hidden) # (B, 16) -> (B, 2)
Все разом це тепер виглядає ось так
import torch.nn as nn
class DenoiserBlock(nn.Module):
def __init__(self, hidden_dim, mlp_ratio):
super().__init__()
self.ln = nn.LayerNorm(hidden_dim)
self.mlp = nn.Sequential(
nn.Linear(hidden_dim, hidden_dim * mlp_ratio),
nn.SiLU(),
nn.Linear(hidden_dim * mlp_ratio, hidden_dim),
)
def forward(x):
z = self.ln(x) # спочатку проганяємо вхідний тензор крізь нормалізацію
return self.mlp(z) # а потім крізь MLP
class Denoiser(nn.Module):
def __init__(self, hidden_dims, num_blocks):
super().__init__()
self.input_encoder = nn.Linear(2, hidden_dims)
block_list = [DenoiserBlock(hidden_dims, 4) for _ in range(num_blocks)]
self.blocks = nn.ModuleList(block_list)
self.output_decoder = nn.Linear(hidden_dims, 2)
def forward(self, x):
hidden = self.input_encoder(x) # (B, 2) -> (B, 16)
for block in self.blocks:
# УВАГА: це залишкова (residual) мережа, тобто
# після кожного шару ми оновлюємо наше приховане представлення додаючи до нього результат роботи блоку
hidden = hidden + block(hidden + time_embedding)
hidden = block(hidden) # вихід одного блоку передається на вхід другому
return self.output_decoder(hidden) # (B, 16) -> (B, 2)
Залишилося тільки написати код для тренування
На самому початку треба сформувати датасет:
BATCH_SIZE = 128
simple_dataset = TensorDataset(make_simple_dataset(4096))
data_loader = DataLoader(dataset=simple_dataset,
batch_size=BATCH_SIZE,
shuffle=True)
Коротше, data_loader — це ітератор по датасету з 4096 елементів, який буде за раз повертати по 128 елементів з цього датасету, в випадковому порядку (але без повторень). Якщо всі елементи закінчаться, то просто почне спочатку.
Саме тренування, це ось такий цикл:
for x, in data_loader:
# одна ітерація тренування
А чому x, а не просто x без коми? Та тому, що data_loader повертає список, адже датасети зазвичай складаються з пар типу (питання -> відповідь) або (зображення -> опис).
Один раз пройти по датасету часто буває недостатньо. Модель повинна побачити один і той же семпл кілька разів. Один прохід по датасету називається епоха (epoch). Тому обгортаємо код в ще один цикл:
EPOCH = 2000
for epoch in range(EPOCH):
epoch_loss = 0 # щоб відстежувати яка сумарна помилка за епоху
for x, in data_loader:
# одна ітерація тренування
# накопичуємо epoch_loss
if epoch % 100 == 0: # пишемо в консоль кожні 100 епох
print(f"Epoch {epoch + 1} completed. Loss: {epoch_loss:.2f}")
Давайте тепер додамо модель для тренування:
LR = 3e-4 # Learning rate. Наскільки сильно за раз будемо оновлювати ваги моделі
DEVICE = "cuda" # Ну не на CPU же.
# ініціалізуємо модель з 8 блоками всередині
model = Denoiser(hidden_dims=16, num_blocks=8)
model.to(DEVICE) # і відправляємо ваги моделі на GPU
# оптимізатор, який буде по-розумному оновлювати ваги у моделі (з інерцією і т.п.)
optimizer = torch.optim.AdamW(model.parameters(), lr=LR)
EPOCH = 2000
for epoch in range(EPOCH):
epoch_loss = 0 # щоб відстежувати яка сумарна помилка за епоху
for x, in data_loader:
# тут підготовка даних для моделі
# створення xt і true_vector на основі семпла x іншими словами
# проганяємо вхідні дані крізь модель і отримуємо передбачення
predicted_vector = model(xt)
# порівнюємо передбачений моделлю вектор з еталонним і обчислюємо помилку
loss = torch.mean((true_vector - predicted_vector) ** 2)
optimizer.zero_grad() # очищаємо градієнт, що залишився з попереднього циклу
loss.backward() # обчислюємо градієнт методом backpropagation
optimizer.step() # оновлюємо ваги
if epoch % 100 == 0: # пишемо в консоль кожні 100 епох
print(f"Epoch {epoch + 1} completed. Loss: {epoch_loss:.2f}")
Багато існує статей, де докладно розписаний механізм зворотного поширення помилки, тому опишу все дуже просто, пропускаючи важливі подробиці.
Загалом, ось цей код створює граф обчислень, в якому збережені всі обчислення, які відбулися, коли дані через модель:
predicted_vector = model(xt)
loss = torch.mean((true_vector - predicted_vector) ** 2)
Отриманий тензор loss теж є частиною цього графа, і тому, коли ми викликаємо
loss.backward()
PyTorch використовує наявний граф обчислень, щоб визначити (обчислити) як повинні змінитися параметри всіх тензорів, що беруть участь в графі, щоб значення loss стало меншим. Похідну обчислює, коротше. Після цього у кожного параметра всередині моделі з'явилося ще додаткове число, яке і є цією похідною. Це і називається градієнт. Тепер за справу береться optimizer. Він має доступ до всіх параметрів моделі (подивіться як він ініціалізувався), а значить і до градієнта. Команда optimizer.step() змушує оптимізатор оновити всі параметри в моделі керуючись градієнтом, learning rate і своїм внутрішнім станом (хитро обчислювана інерція). До речі, зауважте, що параметри оновилися, але градієнт нікуди не дівся і так і залишився прив'язаний до параметрів. Тому, в наступному циклі і викликаємо optimizer.zero_grad(), щоб очистити його, інакше loss.backward() накладе старий градієнт на новий. Це іноді буває корисно, але в такі подробиці вдаватися не будемо.
Дописуємо решту частини циклу:
BATCH_SIZE = 128
LR = 3e-4
DEVICE = "cuda"
EPOCH = 1000
for epoch in range(EPOCH):
epoch_loss = 0
for x, in data_loader:
# копіюємо семпл на GPU
x0 = x.to(DEVICE) # (128, 2) - форма тензора
# створюємо семпл з випадкового розподілу. Теж (128, 2)
noise = torch.randn_like(x, device=DEVICE) # відразу ж опиниться на GPU
# а це вже семпли з рівномірного розподілу в інтервалі від 0 до 1
time = torch.rand((BATCH_SIZE, 1), device=DEVICE) # (128, 1)
# Який вектор треба додати до шуму, щоб отримати цільовий розподіл
true_vector = x0 - noise # відразу 128 векторів за раз
# xt — це точки, що лежать «на півдорозі» від цільового розподілу до нормального
xt = noise + true_vector * (1 - time)
predicted_vector = model(xt)
loss = torch.mean((true_vector - predicted_vector) ** 2)
epoch_loss += loss.item() # накопичуємо помилку для логування
optimizer.zero_grad()
loss.backward()
optimizer.step()
if epoch % 100 == 0:
print(f"Epoch {epoch + 1} completed. Loss: {epoch_loss:.2f}")
Яка у нас задача під час тренування? Є семпли з цільового розподілу x0, є семпли з нормального розподілу noise. Щоб навчити модель трансформувати шумний розподіл в цільовий ми створюємо набір даних xt — це точки, що лежать десь на траєкторії від шумного (нормального) розподілу до цільового. Ось ви запитаєте, а яка у кожної точки траєкторія взагалі? Тут просто, насправді: для кожного семпла з цільового розподілу ми беремо відповідний йому (просто співпавший за індексом) семпл з нормального розподілу. Так як це розподіл випадковий, то можна просто сказати, що кожному семплу (точці) з цільового розподілу береться випадкова точка з нормального розподілу. Не найближча, а просто випадкова, так. В такому випадку true_vector — це просто вектор, що з'єднує цю пару точок. І таких пар 128 — за розміром батча. Тепер раз у нас є точки (семпли) з випадкового розподілу і вектори, які вказують напрямок до (якогось) семпла з цільового розподілу, нам нічого не варто створити набір точок, що лежить на траєкторії від точок випадкового розподілу до точок цільового — просто додати до точок випадкового розподілу відповідний вектор, попередньо його масштабувавши (10% або там 87%). Змінна time з випадковими числами від 0 до 1 як раз для цього. Так і отримуємо набір даних xt який і згодовуємо моделі:
xt = noise + true_vector * (1 - time)
predicted_vector = model(xt)
Якщо цікаво чому (1 - time), а не просто time, то це ми прив'язуємося до того, що чим більше time тим більше шуму.
Тепер код навчання готовий, але якщо ми спробуємо запустити цей модуль, то в результаті лише побачимо з десяток записів в консоль. Ми навіть модель не зберігаємо для подальшого використання. І найголовніше — не бачимо підтвердження того, що моделюєма нами трансформація простого розподілу в складне взагалі працює. Що робити? Написати код семплювання (інференсу), де ми будемо використовувати натреновану модель, щоб витягувати семпли з цільового розподілу (сподіваюся).
Гаразд, ось код інференсу:
samples = torch.randn((400, 2), device=DEVICE)
with torch.no_grad():
STEPS = 50
for step in range(STEPS, 0, -1):
predicted = model(samples)
samples += predicted * (1 / STEPS)
Що тут відбувається? Ми генеруємо семпл з випадкового розподілу, потім 50 разів проганяємо його крізь модель кожного разу уточнюючи вектор predicted. Після кожної ітерації циклу samples стають все ближче і ближче до цільового розподілу, ну
а torch.no_grad() вимикає обчислення градієнта. Корисно, якщо ми хочемо займатися інференсом прямо під час тренування і не хочемо, щоб тестовий прогін моделі якось на цю тренування впливав.
Залишилося лише нанести точки на графік, попередньо імпортувавши pyplot:
import matplotlib.pyplot as plt
Додаємо точки на графік:
samples = torch.permute(samples, (1, 0)).cpu().detach() # (400, 2) -> (2, 400)
plt.figure(figsize=(6, 6))
plt.xlim(-3, 3)
plt.ylim(-3, 3)
plt.grid(True)
plt.axhline(0, color='black', linewidth=0.5)
plt.axvline(0, color='black', linewidth=0.5)
plt.scatter(samples[0], samples[1], s=4, c='blue')
plt.show()
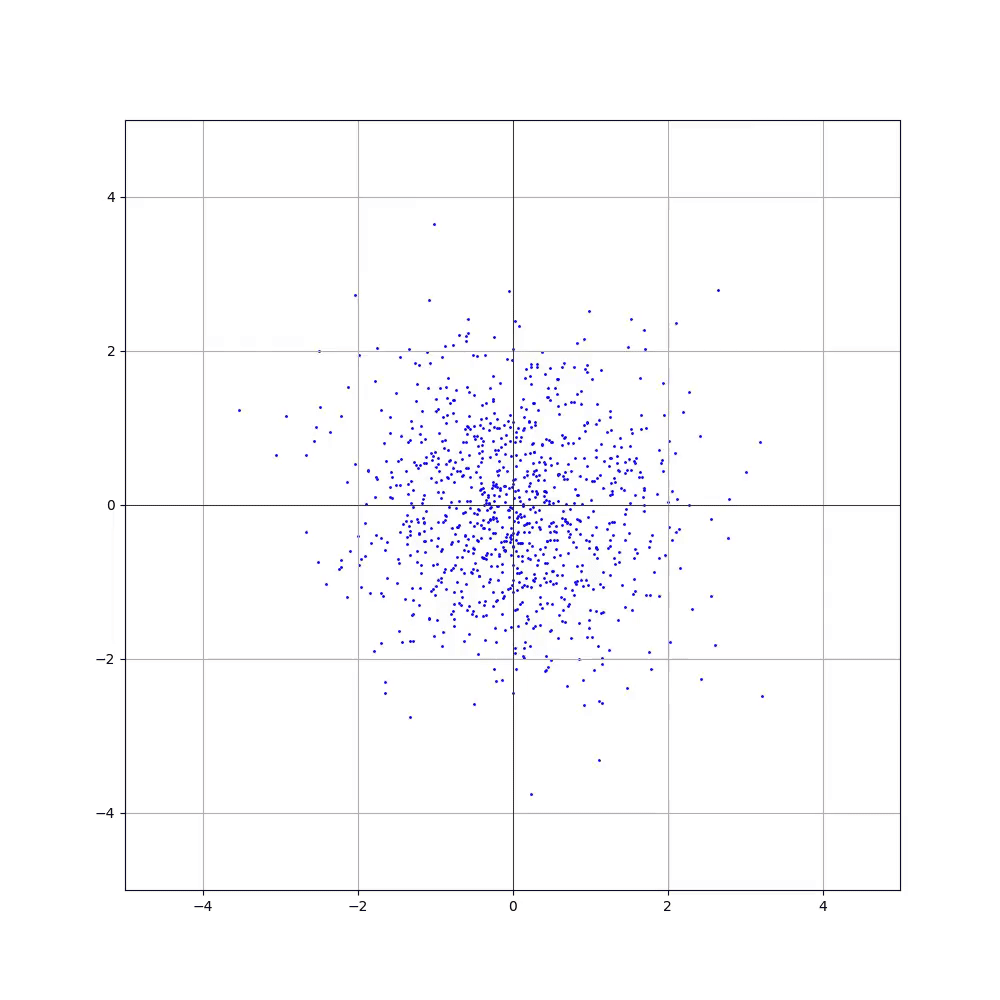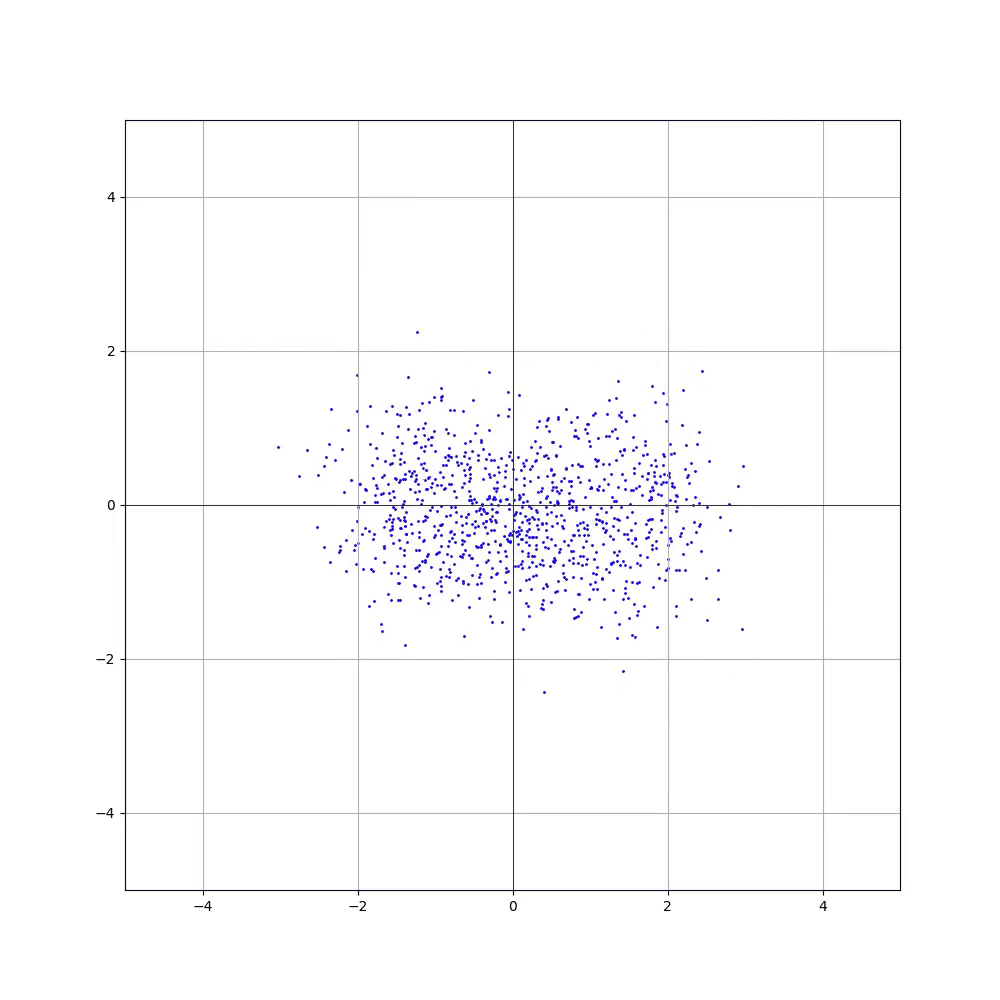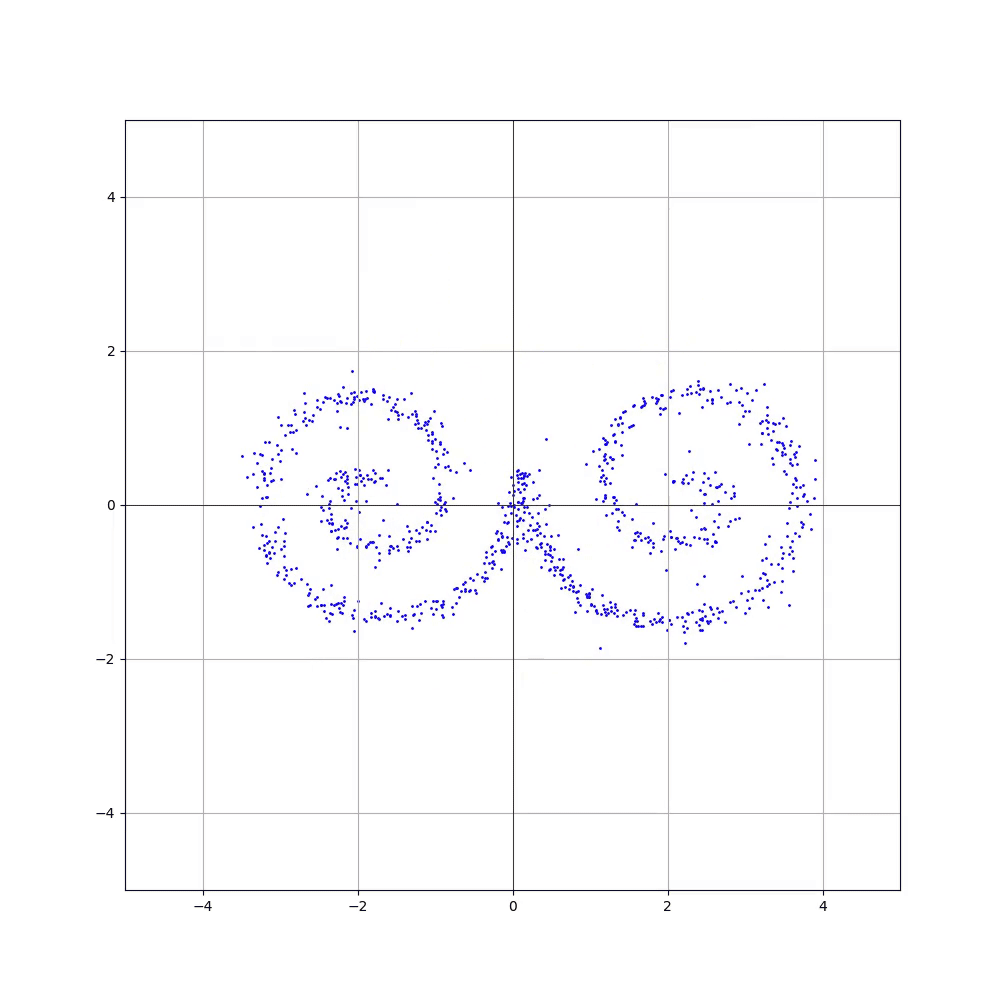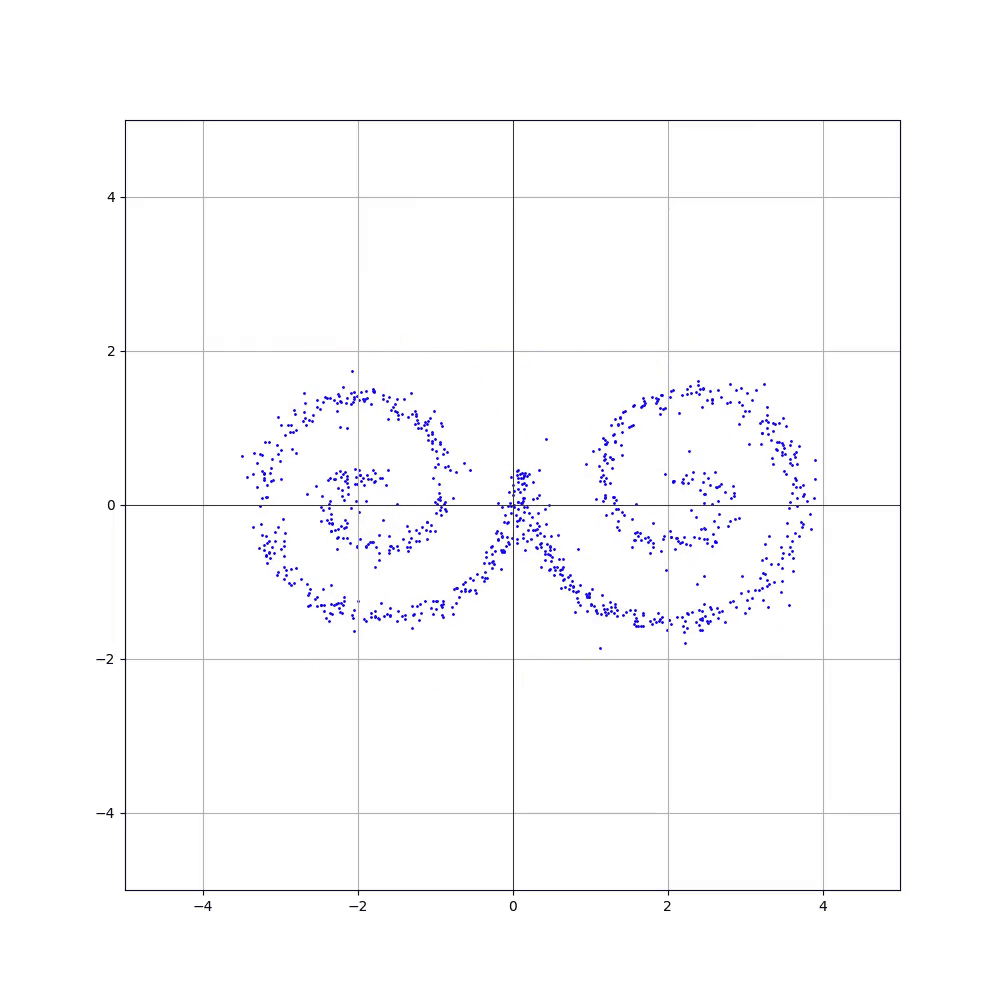
І в результаті отримуємо ось таку візуалізацію (порівняння з цільовою):
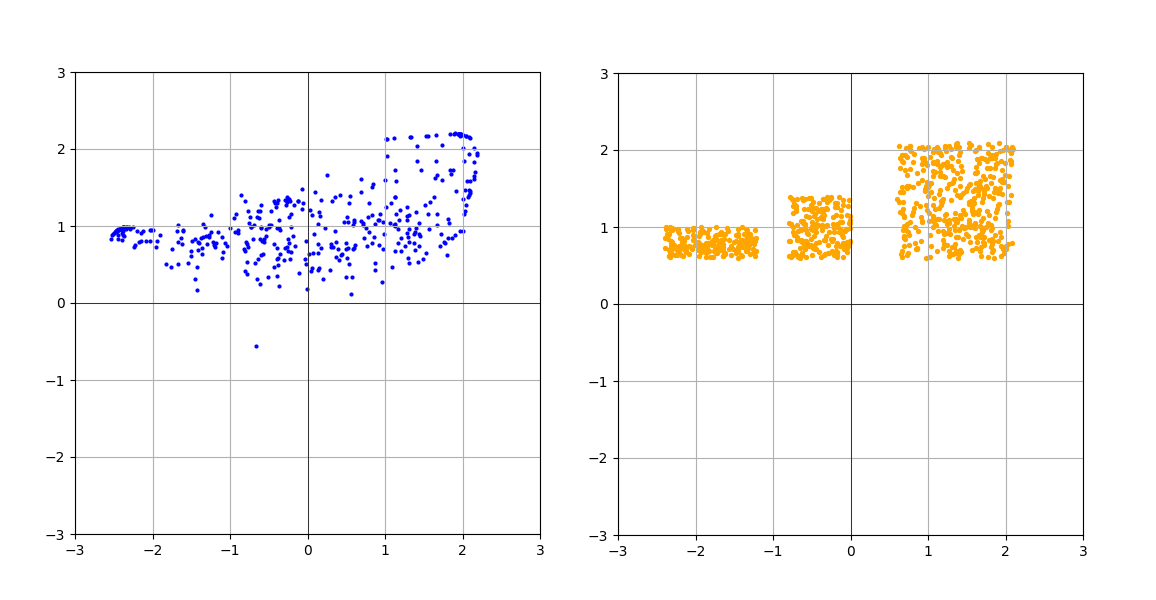
Отже, сьогодні ми навчилися проекту... Зачекайте-но! Ось вам не здається, що ми щось пропустили, ні? Уважний читач вже здогадався — наша модель повністю ігнорує змінну time. А це значить модель вчилася передбачати цільовий розподіл не отримуючи додаткової інформації про те, на якій ділянці траєкторії знаходилися передані їй семпли. Не дивно, що замість цільового розподілу на графіку клякса якась!
Ок, нам треба якимось чином передати в модель інформацію про час (крок). На руках у нас тільки число від 0 до 1, але модель прості числа не перетравлює — потрібно векторне представлення. Для простоти скажемо що вектор повинен бути 16-розмірним — такої ж довжини як і приховане представлення моделі. Отримавши цей вектор (time_embedding) унікальний для кожного числа в інтервалі від 0 до 1, ми просто будемо додавати його до прихованого представлення на кожному рівні, ось так:
hidden = hidden + block(hidden + time_embedding)
Таким чином, «впечатуючи» в приховане представлення інформацію про те, на якому рівні «зашумлення» знаходяться передані в модель дані. Нагадаю ще раз, це потрібно для того, щоб моделі було легше моделювати трансформацію розподілів — адже тепер вона зможе виявляти закономірності між рівнем шуму (time) і переданими даними, таким чином навчаючись краще (в теорії).
Тільки тепер проблема: як же нам з числа отримати 16-розмірний вектор? Я хотів тут написати про sinusoidal і інші експоненти, але, якщо чесно, то простої проєкції вистачить.
Додаємо всередину конструктора Denoiser:
self.time_linear = nn.Sequential(
nn.Linear(1, hidden_dims),
nn.LayerNorm(hidden_dims)
)
LayerNorm просто щоб вихідні значення були десь в районі [-2, 2].
Змінюємо forward метод:
def forward(self, x, t): # тепер на вхід приймає і час
hidden = self.input_encoder(x) # (B, 2) -> (B, 16)
# робимо його меншим, щоб інформації про час було
# але при цьому не «перезаписати» саме приховане представлення
time_embedding = self.time_linear(t) * 0.02
for block in self.blocks:
hidden = hidden + block(hidden + time_embedding)
return self.output_decoder(hidden)
Залишилося лише поправити код інференсу
samples = torch.randn((400, 2), device=DEVICE)
with torch.no_grad():
STEPS = 50
for step in range(STEPS, 0, -1):
# тензор з шейпом (1)
time = torch.tensor(step / STEPS, device=DEVICE)
# розширюємо його до шейпа (400, 1)
time = time.expand(samples.size(0), 1)
predicted = model(samples, time)
samples += predicted * (1 / STEPS)
Запускаємо тренування з тими ж самими параметрами і отримуємо:
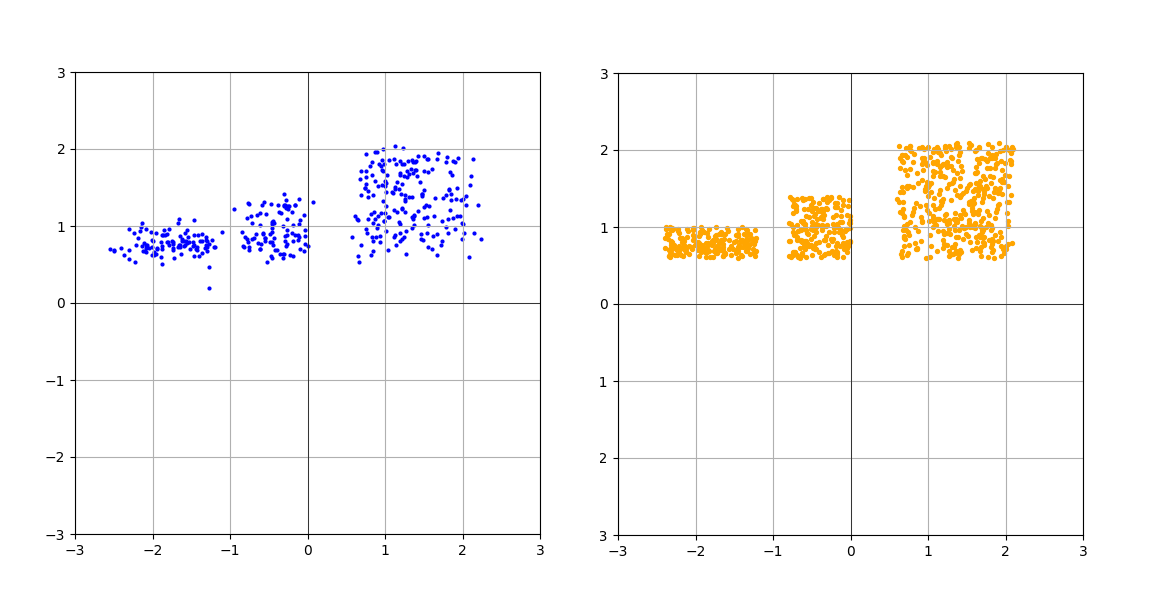
Ось так!
Тут пара анімацій процесу інференсу
Баранів датасет
Важливі деталі:
- Давайте ще раз скажу, модель вивчила не цільовий розподіл, а саме трансформацію нормального розподілу. Якщо запустити інференс з іншим сідом, то точки вже будуть в іншому розташуванні, але все ще в межах цільового розподілу.
- Це не DDPM модель! При DDPM ми б використовували формулу forward diffusion, а тут у нас rectified flow, тому для «зашумлення» семплів ми використовуємо просту лінійну інтерполяцію
xt = x0 * (1 - time) + noise * time. І передбачає модель flow-вектор (velocity), а не шум, як в DDPM. - Весь написаний код можна знайти тут.
Висновок
У цій статті я крок за кроком розповів як з нуля навчити міні-дифузійну модель використовуючи простий синтетичний датасет.
Ключовим моментом стала ідея моделювати трансформацію простого розподілу (шуму) в складний (наш датасет) не за один крок, а покроково, використовуючи Rectified Flow замість DDPM. Це дозволило нам збагатити навчальний набір проміжними станами і створити модель, яка передбачає вектор напрямку (flow-vector) для кожного кроку.
На власному прикладі переконалися, яке важливе значення грає time-embedding для підвищення точності — дозволяє моделі враховувати ступінь зашумлення даних і краще навчатися.
Думаю, я розповів достатньо, щоб у вас з'явилося базове розуміння роботи дифузійних моделей, а значить можна братися за щось цікавіше. Частина 2 буде про навчання вже на датасеті EMNIST. Будемо створювати модель, здатну генерувати малюнки чисел і букв. Продовження слідує...
Коментарі